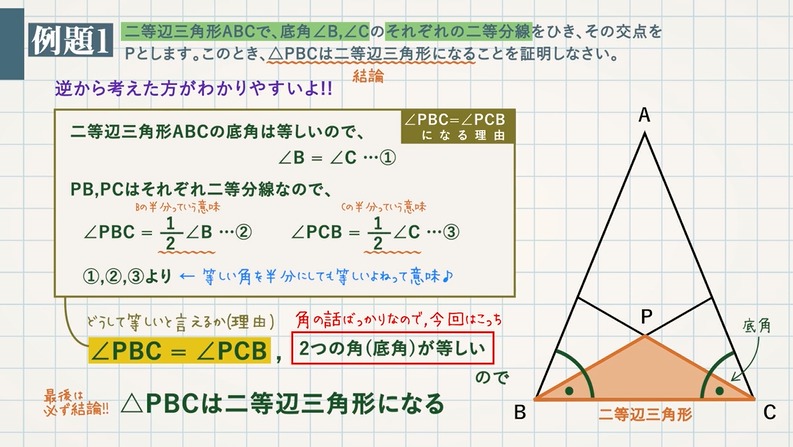
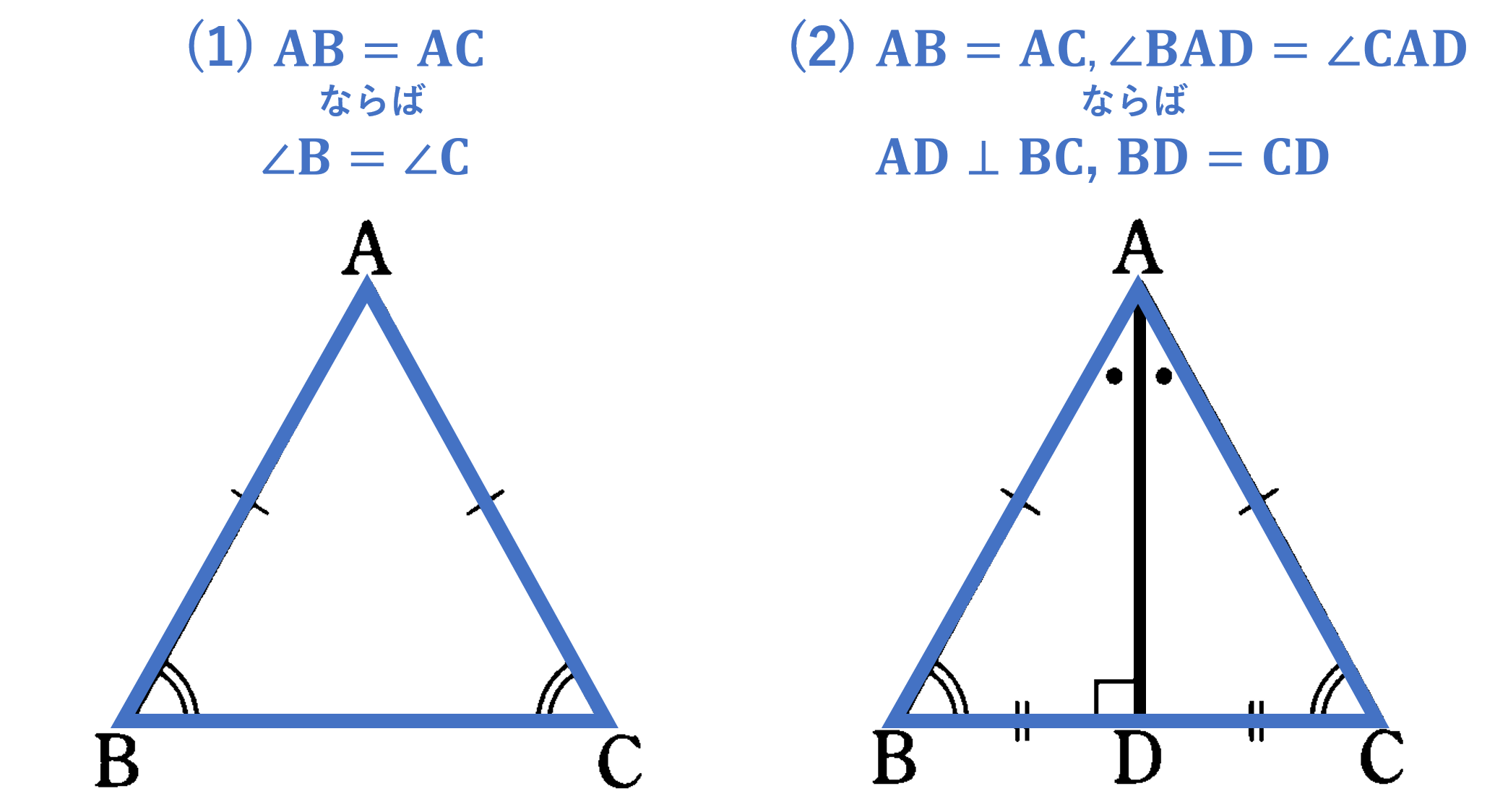
二等辺三角形の底角(定理) 二等辺三角形の底角が等しいことの証明 ab=acの二等辺三角形abcで∠abc=∠acbを証明する。 a b c 証明 d 頂角bacの二等分線をひき、底辺bcとの交点をdとする。 abdと acdにおいて ∠bad=∠cad(角の二等分線) ab=ac(仮定) ad=ad(共通)角の2等分線の定理 定理 BD:DC=AB:AC が成り立つ。 証明 点Cを通り、ABに平行な直線と、ADの交点をEとします。 このとき、 より、 となり、 ACEは、AC=CE の二等辺三角形となります。二等辺三角形の頂角の二等分線は, 底辺を垂直に2 等分する さが等しい 1組の対辺が平行でその長 四角形は、平行四辺形 2つの角が等しい三角形は、その 角を底角とする二等辺三角形 定義 長方形 4つの角がすべて等しい四角形 正三角形 定義3つの

中2数学 二等辺三角形の性質2 頂角の二等分線 練習編 映像授業のtry It トライイット
二 等辺 三角形 定理
二 等辺 三角形 定理-直角二等辺三角形 C言語で図形の面積を求めるプログラムの参考にさせていただきました。 計算式が書いてあるのが親切でいいと思いました。 私もあずま袋を縫いたくて計算しました。 やっぱり50×150がベストっぽい! 小鳥が餌を食べる為の囲いを作る\(\triangle ABC\) が二等辺三角形であることを証明せよ三角形が二等辺三角形であることを示したいとき、・\(2\) つの辺が等しい・\(2\) つの角が等しいのどちらか片方がいえればOKです。これも暗記ですよ。三角形の合同条件を暗記したの同じように。



中2数学 図形の中でも重要なものの1つ 二等辺三角形について徹底解説 まなビタミン
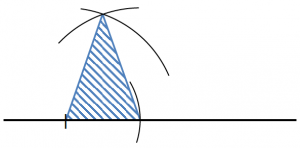
二等辺三角形は、 = となる三角形のことであり、 を頂角、, を底角という。 定理 113 二等辺三角形の底角は等しい。 証明 二等辺三角形を (=) とおこう。このとき、bc の中点を x とおく。直線OA、OP、OBは円の半径なので, OA=OP=OB OA=OPだから、⊿OPAは二等辺三角形。 二等辺三角形の底角は等しいので、 ∠OAP=∠OPA=∠a とおく。 三角形の外角の定理より 直角二等辺三角形の辺の長さの求め方の公式って?? こんにちは!この記事をかいているKenだよ。そぼろごはんはうまいじゃん。 直角二等辺三角形の辺の長さ を計算したいときあるよね? たとえば、 直角二等辺三角形の面積を求めるときとか、
kiepert(キエペルト,キーペルト)の定理: 三角形 a b c abc a bc の外側(または内側)に相似な二等辺三角形 a b f, b c d, c a e abf,bcd,cae a bf, bc d, c a e をつくる。このとき, a d, b e, c f ad,be,cf a d, be, cf は一点 x x x で交わる。 まぁ、三平方の定理でも解けますね。 しかし、もし、4ではなく04などの小数や分数が出た場合は、ちょっと計算が苦しくなります。 あくまでも、一時しのぎと考えて使ってください。 本来は、 比を利用するのがベスト です。 Tweet ← 受験数学:三平方 数学学習の段階番外編:二等辺三角形の底角の定理 どうもシャオムです。 これまで3回に渡って、数学学習の段階について書いてきました。 前回の3回目をもってこれは完結となるのですが、今回は補足として、第2段階の例をもう一つあげておきたい
直角二等辺三角形とは、 二等辺三角形の特徴と直角三角形の特徴をあわせもった三角形 のことです。 直角二等辺三角形の定義 \(3\) つの角のうち、\(2\) つの角がそれぞれ \(45^\circ\) である三角形を「直角二等辺三角形」という。二等辺三角形の選択した2つの入力値から他の要素の値を計算します。 入力指定 底辺と高さ 底辺と斜辺 底辺と底角 斜辺と高さ 斜辺と底角 高さと底角 面積と底辺 面積と高さ 面積と斜辺 面積と底角 高さ(単に「二等辺三角形」と答えると,どの2辺が等しいのか分かりませんので,等しい2辺も書くようにします.) a 2 =b 2 c 2 などは,辺に関する式から角に関する結論を出すものですが,これは中学校で習う三平方の定理の逆なので,簡単に分かるでしょう.




二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学



二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者
この直角二等辺三角形からピタゴラスは「」を発見したと言われているんだ。 もうちょっと具体的にいうと、直角三角形には、 斜辺の2乗は、直角をはさむ辺を2乗して足したものと等しい っていう関係があるんだ。 15 ですので、一見ここは三平方の定理二等辺三角形になるための条件 定理 三角形の2つの角が等しければ、その三角形は等しい2つの角を底角 とする二等辺三角形である。 1 下の図のように、AB=ACの二等辺三角形ABCの辺AB,AC上にそれ「三角形の外角は,それと隣り合わない2つの内角の和に等しい」(重要定理)から, △OBC において ∠BOC の外角 ∠BOA は残り2つの角の和 ∠B∠C に等しいから ∠ BOA=∠ B∠ C (2)




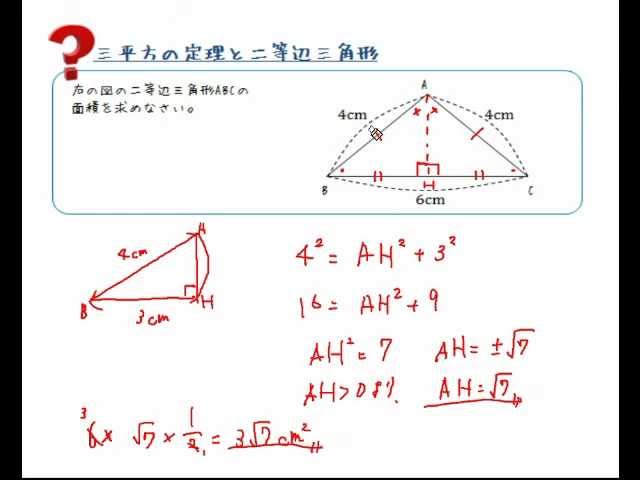
高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ




Mathematics 三平方の定理 3 いろいろな三角形 働きアリ
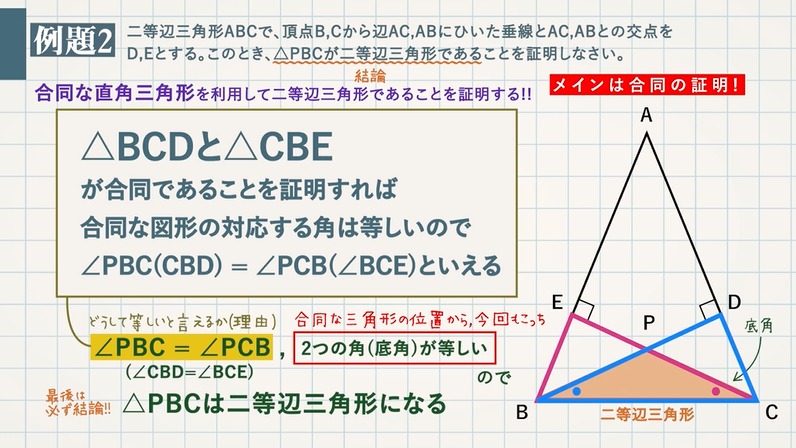
② 逆は「 ABC で,∠B=∠C ならば,AB=AC である。」である。2 つの角が等しい三角 形は二等辺三角形になるので,正しい。 ③ 逆は「2 つの直線 l, m に別の1 つの直線が交わるとき,同位角が等しいならば, l と m は 平行になる。」である。これは正しい。合同条件を示すのに二等辺三角形の性質を用いたいからです。 三辺相等の合同の定理は 他の合同条件にくらべて やっかいなのです。 さて、これで 「二辺挟角」「二角挟辺」「三辺相等」という 2つの三角形が合同になるための 3つの定理が出そろいました。二等辺三角形の定理を証明したいんだけど! こんにちは!この記事をかいているKenだよ。スープは濃いめに限るね。 二等辺三角形の定理にはつぎの2つがあるよ。 底角は等しい 頂角の二等分線は底辺を垂直に2等分する こいつらって、むちゃくちゃ便利。



1




二等辺三角形の角度の問題 基礎から応用までパターン別に解説 中学数学 理科の学習まとめサイト
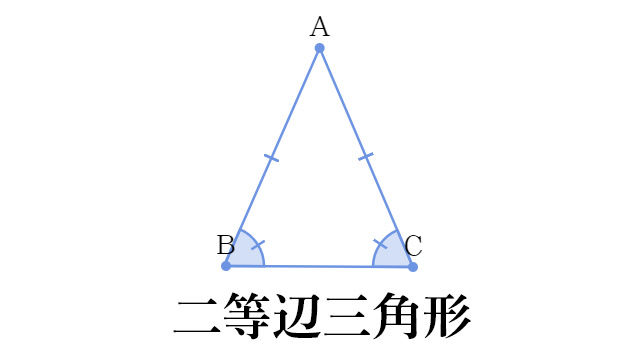
直角二等辺三角形の辺の比は「三平方の定理」から導くことができます。 直角二等辺三角形の底辺と高さの長さは同じです。 底辺(高さ)の長さを「1」として、三平方の定理に代入すると「斜辺 2 =底辺 2 高さ 2 ⇒ 斜辺 2 =11=2 ⇒ 斜辺=√2」になります。二等辺三角形(にとうへんさんかくけい、英 isosceles triangle )は、三角形の一種で、3 本の辺のうち(少なくとも)2 本の辺の長さが等しい図形である。 長さの等しい 2 辺を等辺といい、残りの 1 辺を底辺とよぶ。2 本の等辺が共有する頂点をとくに二等辺三角形の頂点という。 二等辺三角形の定理・性質 二等辺三角形には、\(2\) つの定理(性質)があります。 定理①角度の性質 二等辺三角形の \(2\) つの底角は等しくなります。



二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者




中2数学 二等辺三角形の性質2 頂角の二等分線 練習編 映像授業のtry It トライイット
二等辺三角形 ABC において次のことが成り立っている。 が入れ替わっている。 を入れ替えたものを 逆 という。 ② は ① に逆である。 二等辺三角形である。 正三角形である。 イはアの逆であるがイの文章は正しくない。 二等辺三角形の中には正三角形でないものもたくさんあるからね。 ある定理に対して定理の逆は必ずしも正しいとは限 らない。「定理」とよばれている代表的なものは「円周角の定理」,「三平方の定理」です。 例として「二等辺三角形」で説明してみましょう。 定義二辺が等しい三角形 (図の三角形abcでab=ac) 以下,二等辺三角形の底角を θ \theta θ とし,三角形 A B C ABC A BC の面積を ∣ A B C ∣ ABC ∣ A BC ∣ などと表します。 Kiepertの定理を証明します。チェバの定理の逆を用います。



三平方の定理と二等辺三角形 Youtube



二等辺三角形の定理の証明とその利用
14 二等辺三角形の頂点から対辺に伸びる線分 c ad=√ab×ac−bd×dc 15 メネラウスの定理 c ea ab ×bf fc ×cd de =1 16 チェバの定理 c af fb ×bd dc ×ce ea =1 17 ヘロンの公式d 𝑠= 2 (三角形の面積)= 1 2 √ s(−a )b c 18 トレミーの定理 d ac×bd=ad×bcab×dc 19
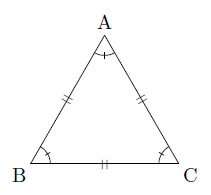



正三角形の性質 まなびの学園



二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者
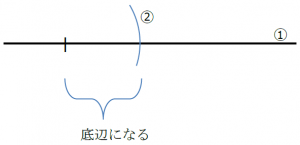



中2数学 図形の中でも重要なものの1つ 二等辺三角形について徹底解説 まなビタミン
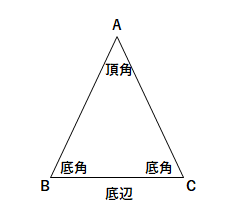



中2数学 二等辺三角形の定義と性質 Examee
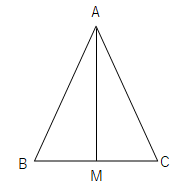



中2数学 二等辺三角形の証明のポイントと練習問題 Pikuu




ม 2 โน ตของ 二等辺三角形の性質 ช น Junior High数学 Clear




中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット




3分でわかる 二等辺三角形の2つの定理 性質 Qikeru 学びを楽しくわかりやすく



5章 三角形と四角形 タカラゼミ




二等辺三角形の定理や性質 底角が等しいことは絶対に覚えよう 中学や高校の数学の計算問題




二等辺三角形の性質 Youtube




高校数学 三角形の形状 正三角形 二等辺三角形 直角三角形 受験の月




数学用語の説明 定義と定理の違いとは 中学数学 定期テスト対策サイト



5章1節02 二等辺三角形の定義と定理 中村 翔




二等辺三角形の定理の証明がわかる3ステップ Qikeru 学びを楽しくわかりやすく




直角二等辺三角形 Wikipedia




中2 二等辺三角形になるための条件 中学生 数学のノート Clear



二等辺三角形の定義と定理




二等辺三角形になることの証明 Youtube
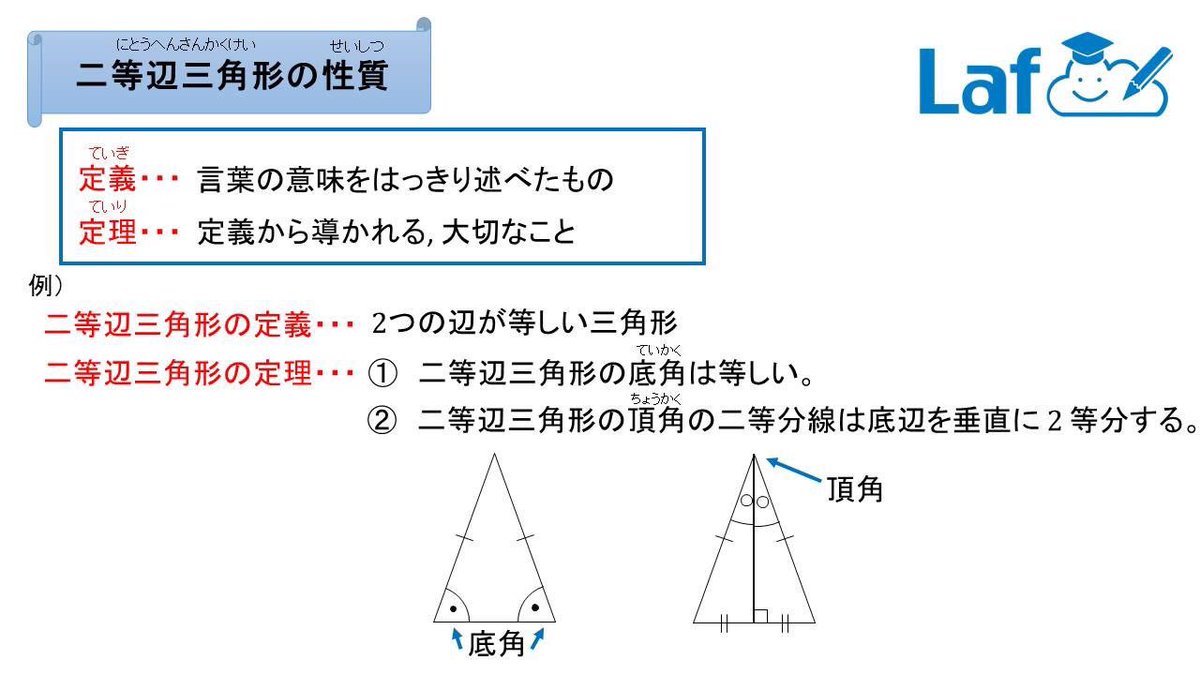



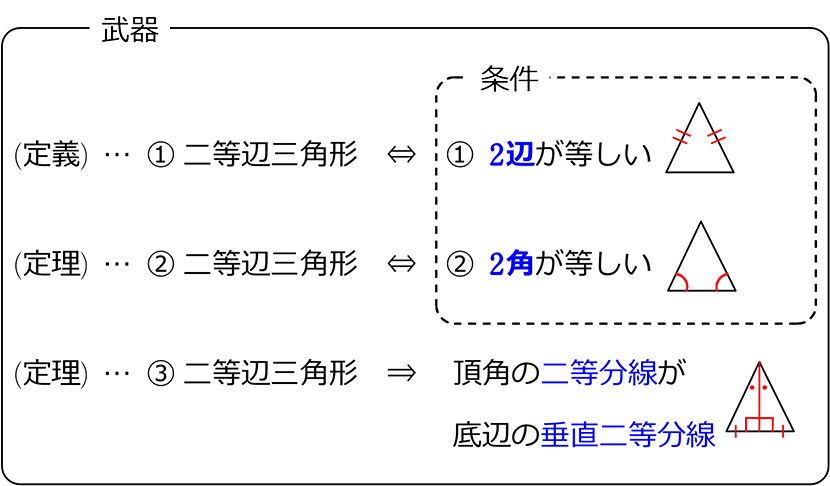
押川 隼也 高校 大学受験対策 على تويتر 中2数学 二等辺三角形の性質 ここでは 定義 と 定理 という小難しい言葉が出てきますね O O 定義 言葉の意味を丁寧に説明したものだよ 二等辺三角形の定義 二つの辺が等しい三角形 定理



今 二等辺三角形が熱い 小学校の算数が懐かしい デイリーポータルz




二等辺三角形の底角は本当に等しいのか ひと筋縄ではいかない証明 ブルーバックス編集部 ブルーバックス 講談社 1 4
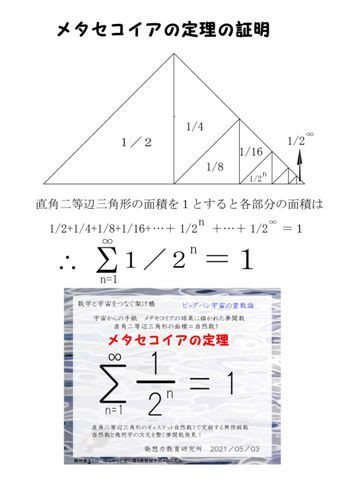



メタセコイアの定理 自然数と直角二等辺三角形の面積を繋ぐ無限級数発見 発想力教育研究所 素数誕生のメカニズム




正三角形や二等辺三角形の内角 Youtube



2




二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比




ม 2 โน ตของ 数学 中2 定義と定理 ช น Junior Clear



2
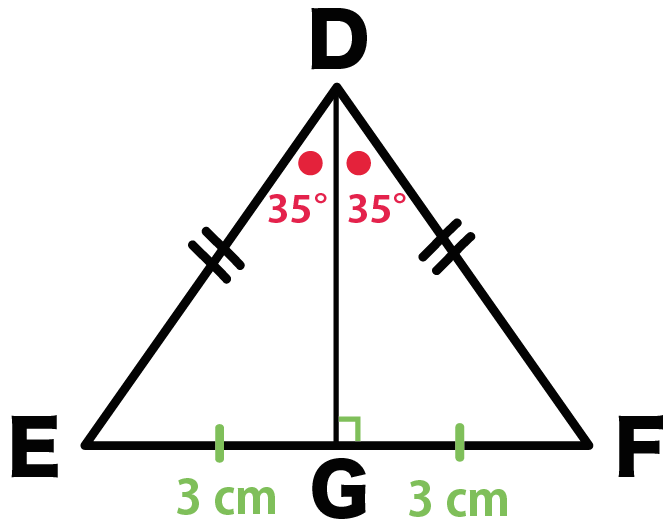



3分でわかる 二等辺三角形の2つの定理 性質 Qikeru 学びを楽しくわかりやすく




中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット



1
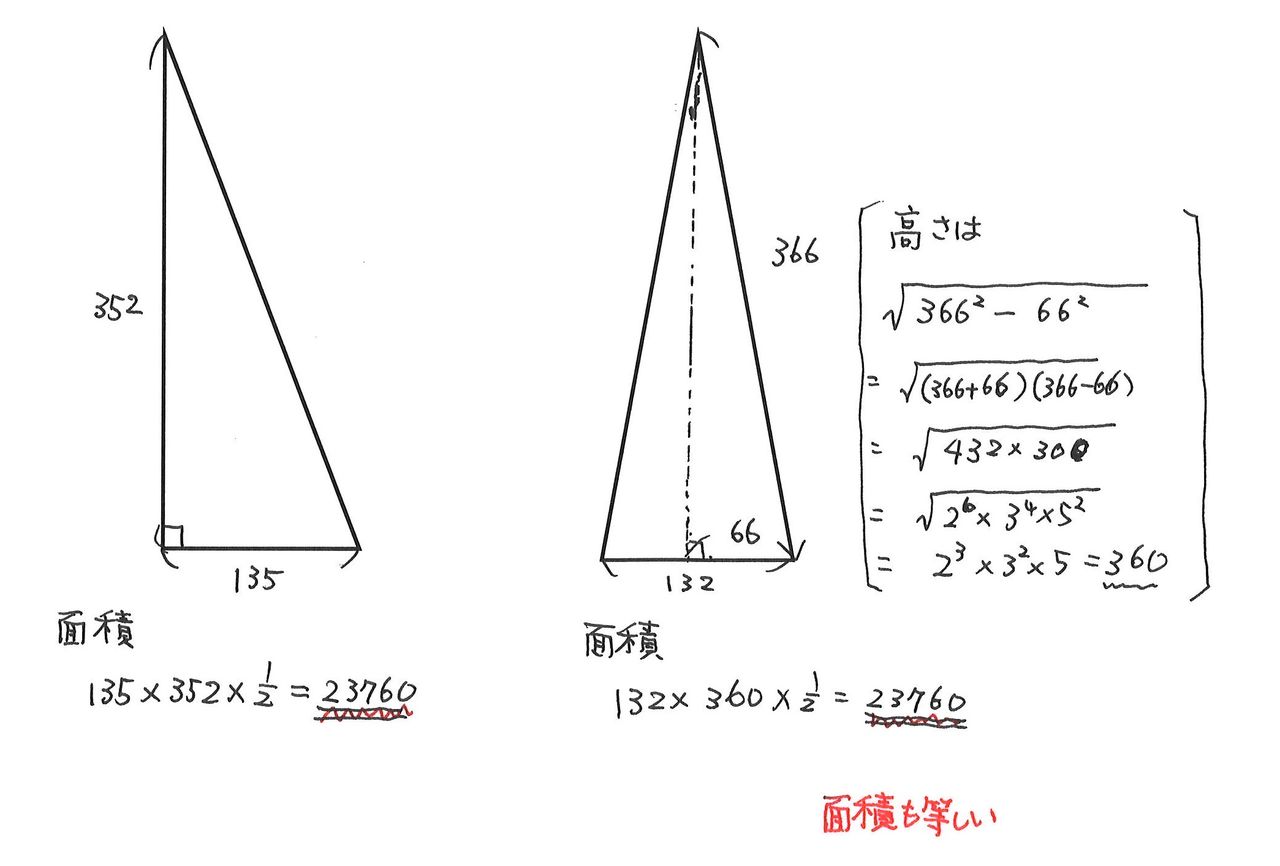



三角形のペア 大田 桐光本部校 ブログ




二等辺三角形の性質の証明 頂角の二等分線 Youtube




二等辺三角形の定義と定理 算数 数学が好きになりmath




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ




二等辺三角形の定理の証明がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中学数学 三平方の定理 直角二等辺三角形 オンライン無料塾 ターンナップ



二等辺三角形と証明 中学2年 数学クラブ




30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学
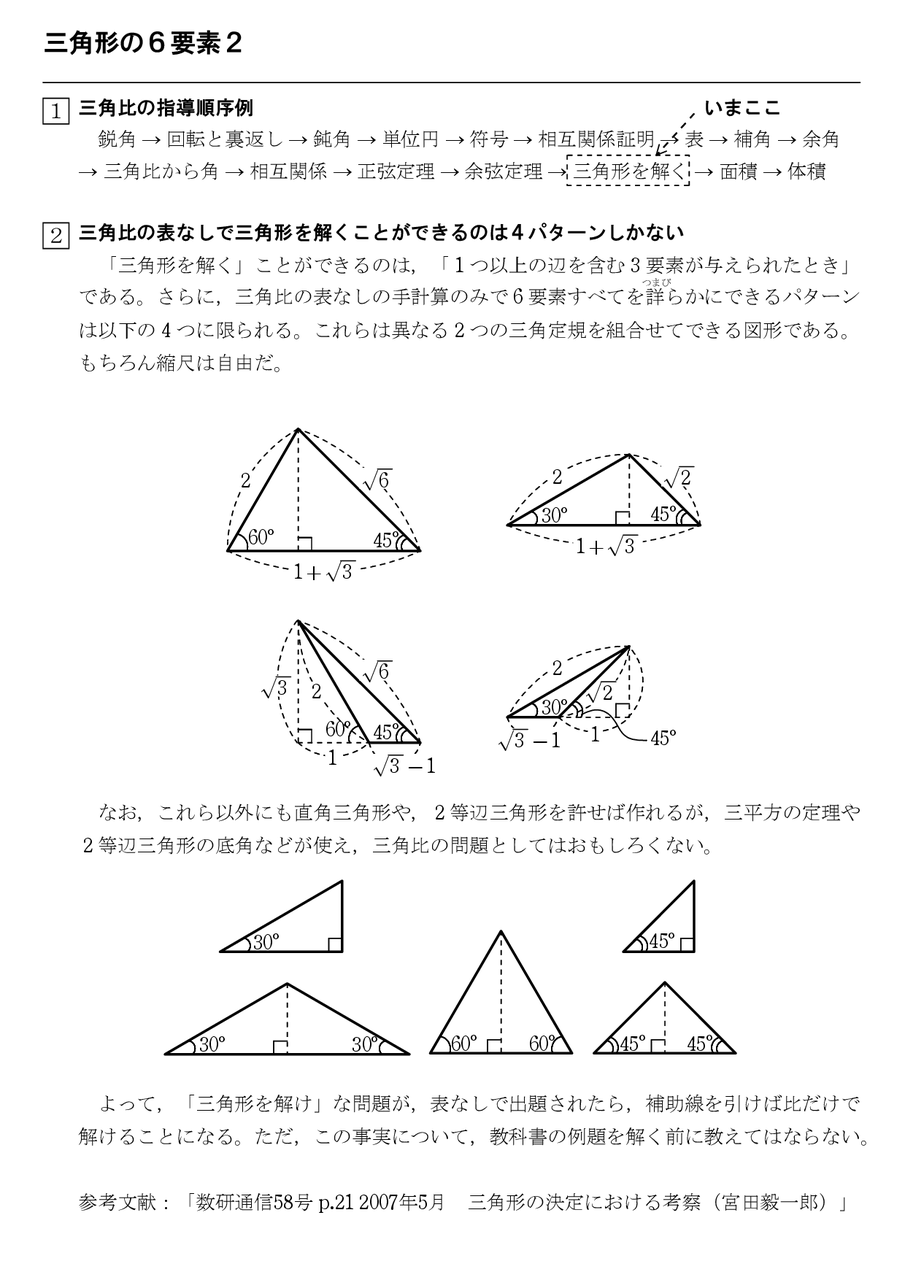



三角形の6要素2 怜悧玲瓏 高校数学を天空から俯瞰する




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ



中学数学 図形の合同 図形の性質




3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ




中2数学 二等辺三角形の証明 例題編 映像授業のtry It トライイット



中2数学 図形の中でも重要なものの1つ 二等辺三角形について徹底解説 まなビタミン



1




二等辺三角形の性質と証明 無料で使える中学学習プリント




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ




二等辺三角形 Wikipedia




二等辺三角形 直角三角形の定義 合同条件と証明問題 リョースケ大学




二等辺三角形の面積




二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者



中2数学 図形の中でも重要なものの1つ 二等辺三角形について徹底解説 まなビタミン




簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
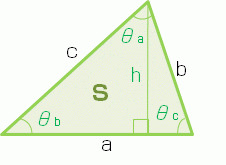



三角形の公式 Wakatta




簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




頂角36度の二等辺三角形の辺の比を教えてください 頂角36度の二等辺三 数学 教えて Goo
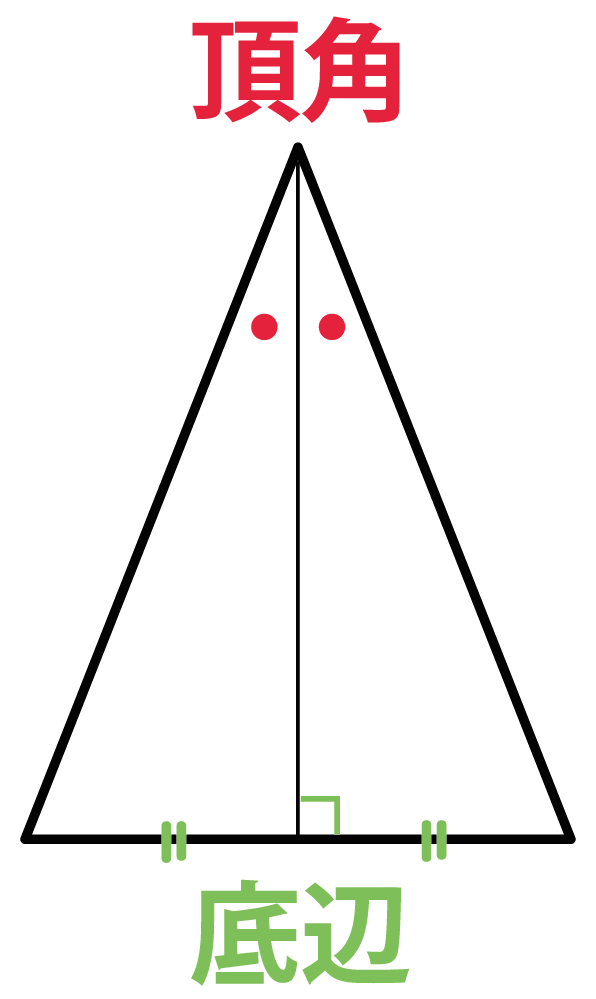



3分でわかる 二等辺三角形の2つの定理 性質 Qikeru 学びを楽しくわかりやすく
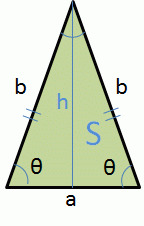



三角形の公式 Wakatta




二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者




中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ




直角三角形の合同条件とその証明 数学fun




中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット




二等辺三角形の頂角の角度を求めよ 解答編その2 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog




中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット
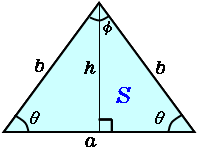



二等辺三角形 高精度計算サイト




世界に1ペアだけ 周りの長さも面積も同じ直角三角形 二等辺三角形 慶大院生ペア証明 朝日新聞デジタル




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ
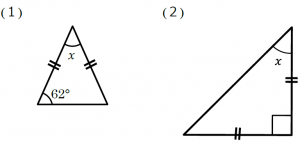



中2数学 図形の中でも重要なものの1つ 二等辺三角形について徹底解説 まなビタミン




二等辺三角形の定理の証明がわかる3ステップ Qikeru 学びを楽しくわかりやすく
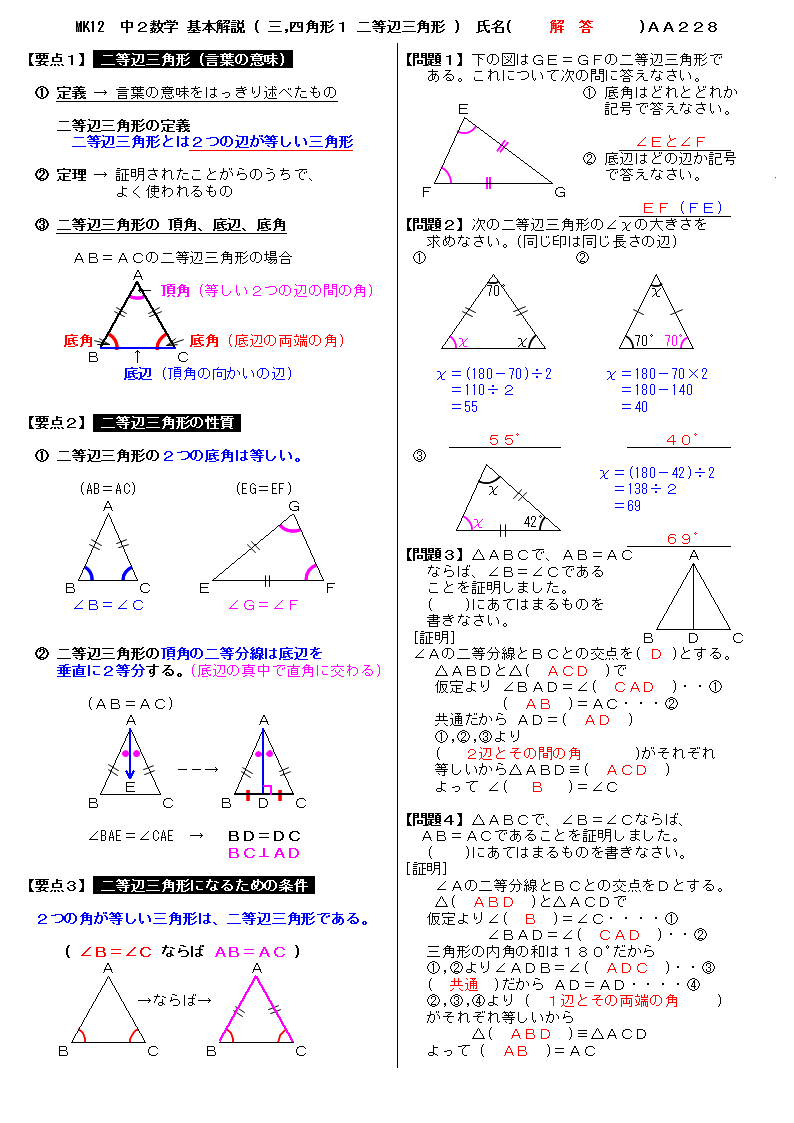



無料 中2数学 基本解説 解答プリント 228 三角形 四角形1 二等辺三角形



二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典




山と数学 そして英語 二等辺三角形の定理と 情報の読み方
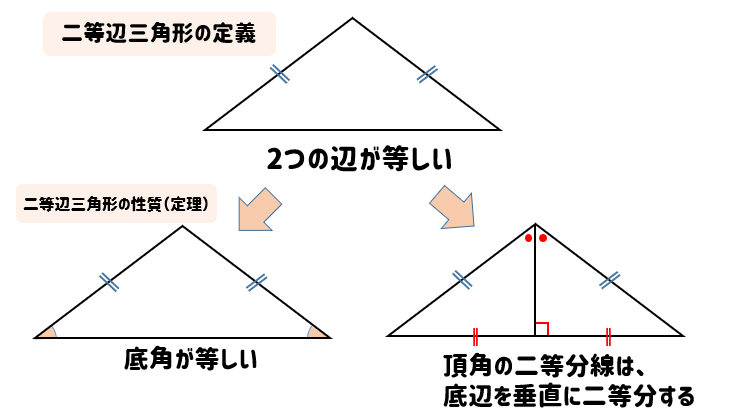



二等辺三角形の定義と性質をサクッと確認しておこう 数スタ
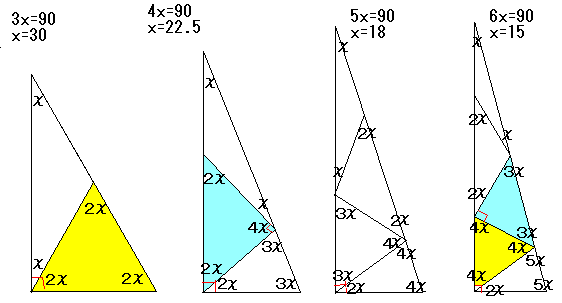



はしご直角三角形




My Math Note




中2数学 図形の中でも重要なものの1つ 二等辺三角形について徹底解説 まなビタミン




ม 2 โน ตของ 中2 数学 二等辺三角形など ช น Junior Clear
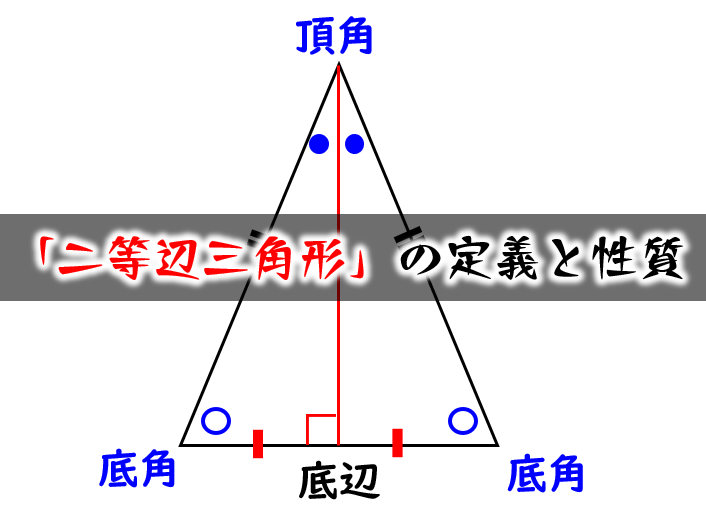



二等辺三角形の定義と性質 問題の解き方 数学fun



二等辺三角形と証明 中学2年 数学クラブ




3分でわかる 二等辺三角形の2つの定理 性質 Qikeru 学びを楽しくわかりやすく



二等辺三角形の底辺は 1分でわかる意味 長さの計算 角度 高さ 三平方の定理との関係
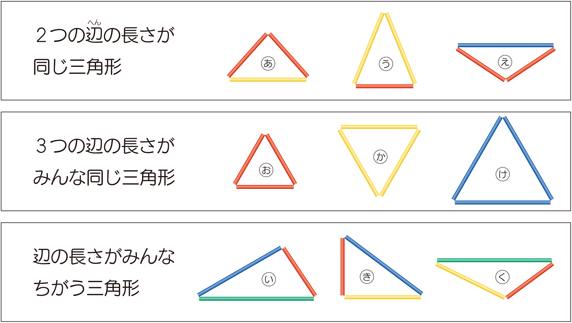



二等辺三角形と正三角形 算数用語集



世界に1つだけの三角形の組 大学院生が定理の証明に成功 数理女子



直角二等辺三角形とは 定義や辺の長さの比 面積の求め方 受験辞典



1




中学数学 三平方の定理 直角二等辺三角形 オンライン無料塾 ターンナップ




中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ




二等辺三角形の斜辺の長さを求めよ 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog




二等辺三角形と正三角形 算数用語集




ピタゴラスの第2定理発見 三平方根の定理 直角三角形の菅数論の定理 発想力教育研究所 素数誕生のメカニズム




直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学




中学2年 数学 図形の性質 二等辺三角形の定理の逆 Youtube


